Table of Contents
Introduction
In general, any assemblage of soil consists of solid particles with voids in between. The solids are small
grains of different minerals, whereas the voids can be filled with either water or other fluid (for example, a contaminant) or with air (or other gas), or filled partly with some of each.

So, the total volume Vt of the soil mass consists of the volume of soil solids Vs and the volume of voids Vv. The volume of voids is in general made up of the volume of water Vw and the volume of air V0 .
A phase diagram shows the three phases separately. It’s as if we could “melt down” all the solids into a single layer at the bottom, then have the water sit on top of that, and finally have the air in a single layer at the top. The phase diagram helps us solve problems involving soil phase relationships. On the left side we usually indicate the volumes of the three phases; on the right side we show the corresponding masses or weights. Even though the diagram is two-dimensional, it is understood that the volume shown is in units of L3, such as cm 3 or ft 3 . Also, since we’re not chemists or physicists, we assume that the mass of air is zero.
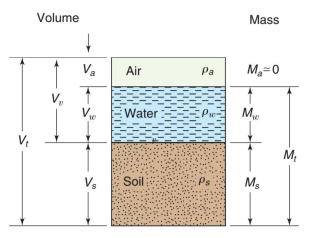
In engineering practice, we usually measure the total volume Vt the mass of water Mw, and the mass of dry solids Ms. Then we calculate the rest of the values and the mass-volume relationships that we need. Most of these relationships are independent of sample size, and they are often dimensionless. They are very simple and easy to remember, especially if you draw the phase diagram.
Three volumetric ratios that are very useful in geotechnical engineering can be determined directly from the phase diagram.
1. The void ratio e is defined as
where Vv = volume of the voids, and Vs = volume of the solids.
The void ratio e is normally expressed as a decimal rather than a percentage. The maximum possible range of e is between 0 and infinity However, typical values of void ratios for sands may range from 0.4 to about 1.0; typical values for clays vary from 0.3 to 1.5 and even higher for some organic soils.
2. The porosity n is defined as
where Vv = volume of voids, and Vt = total volume of soil sample.
Porosity is traditionally expressed as a percentage.The maximum range of n is between 0 and 100%.
it can be shown that
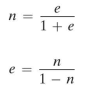
3. The degree of saturation S is defined as
The degree of saturation tells us what percentage of the total void space contains water. If the soil is completely dry, then S = 0%, and if the pores are completely full of water, then the soil is fully saturated and S = 100%.
Now let us look at the other side, the mass or weight side, of the phase diagram in First, we will define a mass or weight ratio that is probably the single most important thing we need to know about a soil-its water content w. It is also the only strictly mass- or weight-based parameter that we’ll define for phase relationships. The water content tells us how much water is present in the voids relative to the amount of solids in the soil, as follows:
where Mw = mass of water, and Ms = mass of soil solids.
or in terms of weights,
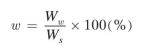
where Ww = weight of water, and Ws = weight of soil solids.
The ratio of the amount of water present in a soil volume to the amount of soil grains is based on the dry mass or weight of the soil and not on the total mass or weight. The water content, which is usually expressed as a percentage, can range from zero (dry soil) to several hundred percent. The natural water content for most soils is well under 100%, although in some marine and organic soils it can range up to 500% or higher.
Applicable ASTM Standard for Soil Water Content
The water content is easily determined in the laboratory. The standard procedure is detailed in ASTM standard D 2216.A representative sample of soil is selected and its total or wet mass or weight is determined. Then it is dried to constant mass or weight in a convection oven at ll0°C. Normally, a constant mass or weight is obtained after the sample is left in the oven overnight. The mass or weight of the drying dish must, of course, be subtracted from both the wet and dry masses or weights. Then the water content is calculated.
The water content may also be determined using an ordinary microwave oven. ASTM standard D 4643 explains the procedure. To avoid overheating the soil specimen, microwave energy is applied for only brief intervals and repeated until the mass becomes nearly constant. A heat sink, such as a glass beaker filled with water, helps to prevent overheating of the soil by absorbing microwave energy after water has been removed from the soil pores. Note that the microwave water content is not a replacement for the oven dry water content but is used when the water content is needed quickly.
Water Content Calculation Example
Given: A specimen of wet soil in a drying dish has a mass of 388 g. After drying in an oven at ll0°C overnight, the sample and dish have a mass of 335 g.The mass of the dish alone is 39 g.
Required: Determine the water content of the soil.
Solution: Set up the following calculation scheme; fill in the “given” or measured quantities a, b, and d, and make the calculations as indicated for c,e, and f.
a. Mass of total (wet) sample + dish = 388 g
b. Mass of dry sample + dish = 335 g
c. Mass of water(a – b) = 53g
d. Mass of dish = 39 g
e. Mass of dry soil(b – d) = 296 g
f. Water content(c/e) x 100% = 17.9%
In the laboratory, masses are usually determined in grams (g) on an ordinary balance. The required sensitivity of the balance depends on the size of the specimen, and ASTM D 2216 gives some recommendations.
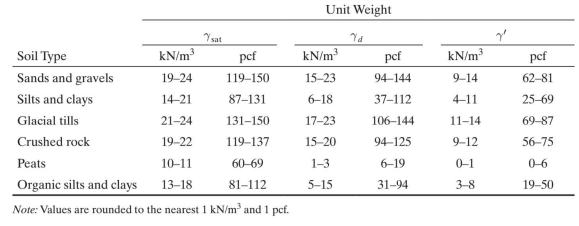
Density of Soil
Another very useful concept in geotechnical engineering is density. You know from physics that density is mass per unit volume, so its units are kg/m 3 . The density is the ratio that connects the volumetric side of the phase diagram with the mass side. Several densities are commonly used in geotechnical engineering practice. First, we define the total, wet, or moist density p;the density of the particles, solid density Ps; and the density of water Pw· We also give the corresponding unit weights, γ, which are obtained by substituting M with the corresponding weight, W.
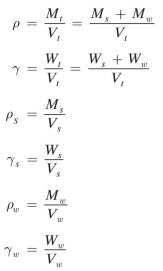
In natural soils, the magnitude of the total density p will depend on how much water happens to be in the voids as well as the density of the mineral grains themselves. Thus, p can range from slightly above 1000 kg/m 3 to as high as 2400 kg/m 3 , with corresponding units weights of 9.81 kN/m 3 ( 62.4 lb/ft 3 ) to 23.4 kN/m 3 (150 lb/ft 3 ). The high end of this range would be essentially solid mineral, with a corresponding density/unit weight close to that of concrete.
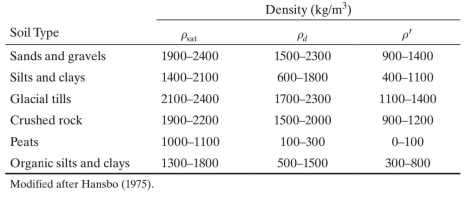
Three other densities very useful in soils engineering are the dry density pd, the saturated density
PsaP and the submerged or buoyant density p’ or Pb, and their corresponding unit weights.

Solution of Phase Problems
Phase problems are very important in soils engineering. As in many disciplines, practice helps; the more problems you solve, the simpler they are and the more proficient you become. Also, with practice you soon memorize most of the important definitions and relationships, so you save time by not having to look them up.
Probably the single most important thing you can do in solving phase problems is to draw a phase diagram. This is especially true for the beginner. Don’t spend time searching for the right formula to plug into. Instead, always draw a phase diagram and show both the given values and the unknowns of the problem. For some problems, simply doing this leads almost immediately to the solution; at least the correct approach to the problem is usually indicated. Also, you should note that there often are alternative approaches to the solution of the same problem.The following steps are recommended to solve these problems:
- List the information you know (from the problem narrative).
- Draw phase diagram, fill in the knowns and the unknowns.
- Try to avoid big formulas.
- If no masses or volumes are given, you can assume either one volume or one mass.
- Fill in one side of the diagram until you get stuck or completely solve it, then “cross over” to the
other side using one of the p’s, ,γ’s, or Gs . - Write out equations in symbol form. Then place the numerical value along with its units in the same order, and solve.
- Check units and reasonableness of your answer.
Soil Phase Problem Example
Given: The definitions of the degree of saturation S, void ratio e, water content w, and the solid density
Ps.
Required: Derive a relationship between S, e, w, and Ps·
Solution: Look at the phase diagram with Vs = 1
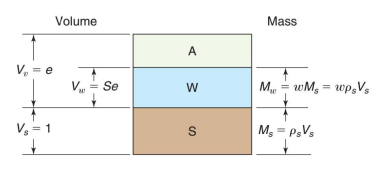
we know that Vw = SVv = Se. From the definitions of water content and Ps, we can place the equivalents for Ms and Mw on the phase diagram. Since Mw = pwVw, we now can write the following equation:
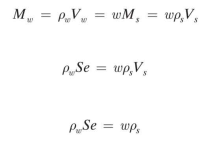
Specific Gravity of Soil
You may recall from physics that the specific gravity G of a substance is the ratio of its unit weight γ to the unit weight of water, usually pure water at 4°C (symbol: γ0),or
Although several different specific gravities can be defined, only the bulk specific gravity Gm , the specific gravity of solids Gs, and the specific gravity of water Gw are of interest in geotechnical engineering. These are defined as
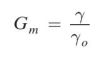

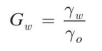
Because the density and therefore the unit weight of water are a maximum at 4°C, the specific gravity of water is exactly 1.0000 at that temperature. Because the value of Gw ranges between 0.9999 at 0°C and 0.9922 at 40°C, it is sufficiently accurate for most geotechnical work to assume Gw = 1.00. Note that specific gravity is a dimensionless quantity and its numerical values are similar to what we used for densities in kg/m 3 divided by 1000. For example, the specific gravity of solid quartz (that is,if we could create a piece that had no void space) is 2.65, and typical values for most soils range from 2.60 to 2.80. Organic soils will have lower specific gravities, while heavy metallic minerals may occasionally have higher values.
If you need to determine the specific gravity of a soil, use ASTM standard D 854.